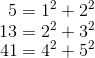Conjetura de Goldbach. Christian Goldbach (1690-1764) conjeturó que:
Todo número natural mayor que 2 y par es igual a la suma de dos números primos.
He aquí algunos ejemplos:
4 = 2 + 2
6 = 3 + 3
8 = 3 + 5
También conocida como la conjetura fuerte de Goldbach ha sido comprobada con la ayuda de las computadoras para los números pares hasta cien millones, pero todavía no ha sido demostrada.
En cambio la conjetura débil de Goldbach la cual afirma que:
Cualquier número mayor que 5 e impar es igual a la suma de tres números primos
Esta ha sido demostrada recientemente por el matemático peruano Harald Helfgott.
Conjetura de Fermat. Pierre de Fermat (1601-1665) conjeturó, en 1637, que:
no existen números enteros que verifiquen la siguiente ecuación para n mayor o igual a 2
La conjetura de Fermat ha permanecido sin demostrar tres siglos y medio. En junio de 1993, el matemático inglés Andrew Wiles anunció que que había demostrado la conjetura de Fermat. Pero su demostración presentaba algunas lagunas, que tardaron más de un año en resolverse. Finalmente, la conjetura de Fermat ha quedado demostrada, convirtiéndose en el gran teorema de Fermat.
Pequeño teorema de Fermat:
2 maneras de expresarlo:
Para cualquier número a y p primo
.
Otra manera de expresarlo es:
Si p es un número primo, y a coprimo con p entonces
.
Ejemplo:
Teorema de Fermat sobre la suma de dos cuadrados:
Todo número primo p se puede escribir como:
,
donde x e y son números enteros si p=2 o p=1 (mod 4).
{5,13,41} son del estilo 4k+1 o dicho de otro modo son congruentes con 1 mod 4
Teorema de Euler (1736)
Si a y n son coprimos entre si
es múltiplo de n.
que en el idioma de los elementos Zn es:
donde 
es la función de Euler, que cuenta los números comprimos con n hasta n.
Teorema de Mills (1947)
Existe una constante
que genera
números primos para cualquier n.
Si la hipótesis de Riemann es cierta el valor de la constante es de = 1,30637788386308069046….
ya que no se conoce ninguna manera de calcular esta constante y se desconoce si el número racional.